[the_ad_placement id=”content”]  

Coordinates and Graphics

Questions

1. A triangle ABC is formed by the points A (3,4), B (-7,2), and C (1,-2).

(a) Find the coordinates of the mid-points k of AB and p of AC                    (1 mk)

(b) Find the equation of the perpendicular bisector of the line kp               (2 mks)

2. The size of an interior angle of a rectangular polygon is 6 ½ times that of its exterior angle.

Determine the number of sides of the polygon.

 

3. The sum of interior angles of two regular polygons of sides n and n + 2 are in the ratio 3:4.

Calculate the sum of the interior angles of the polygons with n sides

 

[the_ad_placement id=”content”]  

4 .        The  area of a rhombus is 60cm². Given that one of its diagonals is 15cm long. Calculate

the perimeter of the rhombus.

 

5. In the figure below AE is parallel to BD. BC = BD, AB = 7.25cm, AE = 15.25cm and

ED = 5.25 cm

Find the perimeter of the figure.

 

6. The figure below shows a trapezium ABCD in which side AB is perpendicular to both AD

and BC.        Side  AD=17cm, DC=10cm

(i) What is the length of side AB

(ii) Find the value of cos(90^o – x^o) in the form a where a   and  b are integers

 

[the_ad_placement id=”content”]  

b

7. The size of an interior angle of a regular polygon is 3x^o while its exterior angle is (x-20)^o.

Find the number of sides of the polygon

 

8.  In the figure above, angle a is half the sum of the other angles. Evaluate the triangle         

 

9. The sum of the interior angles of an n-sided polygon is 1260^o. Find the value of n and

hence deduce the polygon

10. Giving reason, find the angle marked n

11. Solve for y in the equation 125 ^y+1 + 5^3y = 630

[the_ad_placement id=”content”]  

12. The interior angle of a regular polygon is 108^o larger than the exterior angle. How many

sides has the polygon?

 

13. The interior angle of a regular polygon is 4 times the exterior angle. How many sides has

the polygon

 

14. In the figure below ABCD is a trapezium with DC parallel to AB. DC = 5cm, CB = 4cm,

BD = 8cm    and AB = 10cm

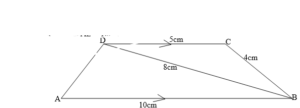
            Calculate:

(a) the size of angle BDC

(b) the area of triangle ABD

 

15. In the figure below, DE bisects angle BDG and AB is parallel to DE. Angle DCF = 60^o

and angle   CFG = 100^o

Find the value of angle:-

(a) CDF

(b) ABD

16. The size of an interior angle of a regular polygon is 4x^o, while its exterior angle is (x – 30)^o.

Find  the number of sides of the polygon

 

17. The sum of interior angles of a polygon is 1440^o. Find the number of sides of the polygon

hence   name the polygon

[the_ad_placement id=”content”]  

18. In the figure below PQ is parallel to RS. Calculate the value of x and y

19. The interior angle of a n-sided regular polygon exceeds its exterior angle by 132^o.

Find the value of n

[the_ad_placement id=”content”]  

Read Also: Angle and Plane